Ⅰ. 서론
인과추론(causal inference)은 특정 사건의 원인과 효과에 대해 분석하는 통계학 분야로 경제학, 정치학, 사회학 등 다양한 학문 분야에서 활용되고 있으며, 사회정책 변화의 효과를 평가하여 향후 정책 수립에 활용되는 등 실험 및 관찰 환경에서 인과 효과를 신뢰성 있게 추정하는 방법론이다(Imbens, 2024). 인과추론의 핵심 목표는 특정 사건이나 변화에 대한 원인을 찾고 또 원인에 의한 변화정도나 영향력을 추론하는 것이다. 이를 위해 외생변수(exogenous variable)를 통제하여 특정 사건이 일어나기 전과 후의 결과를 비교함으로써 인과관계를 파악하고 검증하는 다양한 방법론이 제안되었다(Holland, 1986; Imbens & Rubin, 2015; Rubin, 1974). 사건이 일어난 것을 실험연구에서는 의도적으로 만든 것이기에 처치(treatment)라고 하고, 정책연구에서는 정책의 변화가 일어난 것을 의미해서 개입(intervention)이라고 한다. 본 연구에서는 두 용어를 같은 의미로 혼용해서 사용한다.
인과추론 연구를 위한 전통적인 방법인 실험 설계(experimental design) 혹은 RCT(Randomized Controlled Trials)는 외부환경을 통제하여 특정 사건의 처치 효과를 비교적 명확하게 추정할 수 있으나 일반적으로 통제가 가능한 실험환경은 소규모의 표본 수만을 허용한다. 실험실이 아닌 자연 상태의 상황에서 정책의 변화나 사회적인 변화 등 다수의 사람이 생활하면서 만들어내는 효과를 연구하기에는 현실적인 한계와 윤리적인 문제가 발생할 수 있다. 따라서 실험의 조건을 갖추지 못한 상태에서 활용하는 준실험설계(quasi-experimental design) 혹은 관찰연구(observation Study)가 적용되고 있다(Cham et al., 2024). 준실험설계 방법의 하나인 이중차분법(DID: Difference In Differences)은 특정 사건의 처치 전후의 변화를 이용하여 처치의 효과를 추정하며, 이는 실험군(treatment group)과 대조군(control group)의 시간에 따른 변화를 집단 내, 집단 간, 이중으로 비교함으로써 특정 사건의 처치 효과를 추정하는 방식으로 활용된다. DID 방법은 처치가 없었더라면 두 집단이 유사한 경향을 보였을 것이라는 평행추세를 만족하는 가정하에서, 특정 사건의 처치 후 변화의 순수한 효과를 추정할 수 있으며, 비교 집단 혹은 대조군의 단위가 많은 경우 유용하게 사용되어왔다(손호성, 이재훈, 2018; Arkhangelsky et al., 2021; Athey & Imbens, 2022; Lechner, 2011).
하지만, 정책 개입 평가와 같은 현실적인 상황에서 DID 방법의 가정인 실험군과 대조군의 처치 전 평행추세 조건을 만족하지 못하는 경우가 많아, 선택 편향(selection bias)의 문제가 발생하기도 했다. 이를 해결하기 위한 방법으로 통제집단합성법(SCM 혹은 SC: Synthetic Control Method)이 등장하였다(Abadie, 2021; Billmeier & Nannicini, 2013). SCM은 비교 사례연구를 위한 대안적 접근법으로, 정책이 개입된 지역과 개입되지 않은 지역을 비교하여 정책 개입 전 실험군과 평행추세를 만족하는 가상의 합성대조군을 생성한다. 이를 통해 정책이 개입되지 않았을 때 생길 수 있는 반사실적(counterfactual) 상태를 만들어 실제 정책 개입이 이루어진 지역과 비교함으로써 정책 개입의 효과를 추정한다. SCM은 DID보다 외생변수에 대한 효과적인 통제가 가능하며, 합성대조군을 생성할 때 가중치를 적용하는 방법에 따라 개별 사례 연구나 대조군이 소수의 단위일 때 활용하기 적합하다(이정기, 문정빈, 2020; Doudchenko & Imbens, 2016).
최근에는 DID와 SCM의 장점을 결합한 통제집단합성-이중차분법(SDID: Synthetic Difference In Differences)이 등장하였으며, SDID는 합성대조군을 생성할 때, SCM처럼 정책 개입 전 실험군과 평행추세 가정을 충족시킬 수 있도록 대조군 단위(지역)에 가중치를 만들며, 여기에 더하여, 합성대조군의 정책 개입 전과 후의 평균 차이를 최소화하는 시간 가중치를 적용하여 보다 유연한 분석을 가능하게 한다. 따라서 다양한 상황에서 특정 사건의 개입에 대한 보다 정확하게 영향을 추정할 수 있다(Arkhangelsky et al., 2021).
본 연구의 주요 목적은 DID, SCM, SDID 세 가지 방법을 비교 분석하여, 기존 연구에서 제시한 각 방법의 장단점을 검증하고, 다양한 상황에서의 적용 가능성을 평가하는 것이다. 특히, 다양한 상황에서 모형들이 만드는 다른 결과를 확인하고, 어떤 상황에서 어떤 방법이 더 적합한지를 살펴본다. 이를 검증하기 위하여 다양한 결과 값을 활용하였다. 먼저, 추정치(estimates)와 표준오차(standard error)를 통해 각 방법이 도출한 결과의 신뢰성을 확인하였으며, SCM과 SDID 방법을 위한 처치 전 합성대조군과 실험군의 유사도를 유클리디안 거리(euclidean distance)와 기울기(slope) 비교를 통해 확인하였다. 추가적으로 모형의 적합도와 복잡도를 확인하기 위해 잔차제곱합(sum of squared errors)과 이를 통해 추정한 AIC(akaike information criterion) 값을 확인하였다. 이를 통해 세 가지 방법(DID, SCM, SDID)의 장단점을 보다 체계적으로 검증하고, 각 방법의 적용 가능성을 평가하였다. 분석에 활용한 데이터는 지역 내 새벽배송 서비스 업체의 진입으로 인해 오프라인 상권에 미쳤던 영향을 측정하는 사례를 활용하였다.
본 연구는 인과추론 연구자들에게 학문적 시사점을 제공할 뿐만 아니라, 다양한 연구 영역에서 각 방법의 특성과 적용 가능성을 검토함으로써 연구 상황에 적합한 방법을 선택하는 데 기여할 것이다. 이는 궁극적으로 실무적인 상황에서 보다 정확한 정책 평가뿐만 아니라 적절한 마케팅 전략 수립에도 유용하게 활용될 수 있을 것이다.
Ⅱ. 이론적 고찰
전통적인 연구방법론에서 '순수실험설계'라고 불리는 무작위 대조 실험(RCT)은 참여 대상을 실험군과 대조군에 무작위로 할당하여 표본 추출 과정에서 발생할 수 있는 편향을 줄이고, 처치 효과 외의 두 집단 간 특성을 유사하게 만들어 외생변수를 통제함으로써 인과관계의 순수한 효과를 추정할 수 있도록 설계된 방법이다(Colnet et al., 2024; de Souza Leão & Eyal, 2019; Rubin, 1974). 그러나 정책 연구와 같이 실제 환경에서는 무작위 대조 실험을 수행하는 것이 현실적으로 어렵거나 불가능한 경우가 많았고, 이러한 한계를 극복하기 위해 관찰 데이터(data)를 이용한 인과 추론 연구가 발전해왔다(Cham et al., 2024).
인과추론 연구는 크게 Causal graphic 모형을 통하여 Bayesian network 모형이나 Do operator를 활용한 연구들과 잠재적 결과 체계(potential outcomes framework)로 나눌 수 있으며, 전통적으로 구조방정식(structural equation models)도 인과관계를 연구하는 모형으로 생각해볼 수 있다. 이 중에서 많이 활용되는 연구 분야는 잠재적 결과체계로서, 이는 연구 대상에 대해 특정 처치를 했을 때의 실제 결과와 처치를 하지 않았을 때의 잠재적 결과, 즉 실제로는 관찰하지 못하지만 발생할 잠재성이 있는 결과로 반사실적(counterfactual) 결과와 비교하여 인과 효과를 정량화하는 방법들을 의미한다. 이런 방법을 Rubin의 인과모형(rubin causal model)이라고도 한다. 기본적인 아이디어는 실제로 존재하지 않거나 직접 관찰할 수 없으므로 처치를 받지 않은 대조군을 최대한 실험군과 유사하게 만들어, 선택 편향(selection bias)을 제거하고 외생변수를 통제하여 인과추론의 정확성을 높이는 것을 목표로 한다(Peters et al., 2017).
잠재적 결과체계는 다시 성향 점수(propensity score)에 기반한 연구와 회귀분석에 기반한 연구로 구분될 수 있다. 회귀분석에 기반한 연구들의 대표적인 예로는 회귀 불연속 설계(RDD: Regression Discontinuity Design), 도구변수법(IV: Instrumental Variables), 그리고 이중차분법(DID: Difference in Differences) 방법이 있으며, 각기 다른 가정을 통해 인과적 효과를 추정한다. 특히, DID는 실험군과 대조군의 사전-사후 변화를 비교하여 처치 효과를 추정하며, 정책연구 등 다양한 분야에서 활용되고 있다. 또한, DID의 기본 가정인 실험군과 대조군의 처치(개입) 전 사전 기간에 대한 평행추세를 만족시키기 위한 대조군을 구성하는 방법(SCM, SDID 등)이 개발되면서 복잡한 데이터와 현실 세계의 처치 효과를 분석할 수 있는 장점으로 연구자들의 활용도가 높아지고 있다(Callaway, 2023; Currie et al., 2020). 성향 점수(propensity score)에 기반한 연구는 매칭(matching), IPTW (Inverse Probability of Treatment Weight) 등이 있으며, DID를 수행할 때 성향 점수를 활용하여 대조군을 선별하는데 활용되기도 한다(Stuart et al., 2014).
잠재적 결과체계 모형에서는 처치 혹은 개입의 전후를 비교하면서 효과를 측정하며, ATE(Average Treatment Effect)와 ATT(Average Treatment Effect on the Treated)를 주요 지표로 사용한다. ATE는 처치를 받은 집단의 평균 결과 Y(1)와 처치를 받지 않은 집단의 평균 결과 Y(0)의 차이로 처치의 효과를 측정하는 지표이다. 그러나 처치를 받은 집단과 받지 않은 집단들이 모든 조건에서 동일하도록 만들 수 없기 때문에 이론적으로는 타당하지만 실제 연구에서는 ATT가 더 많이 활용된다. ATT는 처치를 받은 집단의 처치 후 결과 (Y(1)∣D=1)와 처치를 받은 집단이지만 처치를 받지 않았을 경우의 결과인 (Y(0)∣D=1)의 차이를 의미한다. 그러나, 처치를 받은 집단에서 처치를 받지 않았을 경우의 결과는 실제로는 일어나지 않은 반사실적 결과이므로, 실제 연구에서는 처치를 받지 않은 집단인데, 모든 조건은 처치받은 집단과 거의 동일한 집단의 결과인 (Y(0)∣D=1)를 활용한다. 조금 다른 개념으로 ATU(Average Treatment Effect on the Untreated)도 있다. 이것은 처치를 받지 않은 집단에서 처치를 받은 효과를 찾는 개념이다. ATE와 ATT의 수식은 다음과 같다.
-
Y(1): 처치를 받은 경우의 결과
(특정 사건의 개입 후).
-
Y(0): 처치를 받지 않은 경우의 결과
(특정 사건의 개입 전).
-
D=1: 처치를 받은 개체
(특정 사건이 일어난 지역, 단위).
잠재적 결과체계에서의 실험군의 결과는 처치를 받은 (Y(1)∣D=1)이며, 대조군의 결과는 (Y(0)∣D=1)이 된다. ATT는 실제로 처치를 받은 집단에 대한 효과를 측정하여 정책이나 프로그램의 실질적 영향을 평가하는 데 유용하며, 관찰연구에서 선택 편향을 줄인다. 또한, 특정 집단에 대한 구체적인 통찰력을 제공하고 있으며, 본 연구에서는 사례를 통한 분석으로 특정 사건의 개입이 있는 지역과 그 외 지역을 비교하여 개입의 효과를 추정하는 ATT를 활용하고자 한다.
DID는 1980년대에 경제학 분야에서 정책 변화를 평가하기 위해 개발된 방법으로, Card and Krueger(1993)의 연구에서 뉴저지주의 최저임금 인상이 패스트푸드점 고용에 미친 영향을 분석하는 데 활용하면서 대중화되기 시작했다. 이후 경제학, 사회과학, 보건학 등 다양한 분야에서 정책 평가, 치료 약 효과 분석, 프로그램 효과 분석, 사회 현상 이해 등에 활용되고 있다(곽기호, 2019; 김난영, 2019; Callaway, 2023; Rothbard et al., 2024). 최근에는 빅데이터(big data)의 발전과 함께 DID를 활용한 연구가 증가하는 추세를 보이고 있다(Currie et al., 2020; Fredriksson & Oliveira, 2019).
DID는 특정 사건의 처치 전, 후로 실험군과 대조군의 차이를 비교하는 방법으로 특정 사건의 처치 효과를 추정하며, 시간에 의해 변하지 않는 요인을 통제하는 반면 시간에 의해 변하는 요인을 통제하지 못하기 때문에 특정 사건 이전 실험군과 동일한 경향(parallel trend assumption)을 가지는 대조군을 설정하여 시간에 의해 변하는 요인을 통제한다(Lechner, 2011). 또한, 두 집단이 동일한 시점에 특정 사건이 발생하고 연구기간 동안 두 집단 내 구성원은 유지되어야 하는 것을 전제로 한다(Imbens & Wooldridge, 2009).
DID의 추정량은 개념적으로 아래 식(3)과 같이 실험군의 특정 사건인 처치 후와 처치 전 간의 결과 변수 평균값의 차이에서 대조군의 특정 사건인 처치 후와 처치 전 간의 결과 변수 평균값의 차이를 빼는 것으로 특정 사건의 처치 효과를 추정한다.
DID 추정값은 일반적으로 식(4)와 같이 선형 회귀식을 통해 추정된다. β0는 처치 전 대조군의 평균 결과를 의미한다. β1는 Postt의 계수로 처치로 인한 평균 변화량을 나타내며, β2는 Treati의 계수로, 실험군과 대조군 간의 기본적인 차이를 나타낸다. τ는 상호작용 항의 계수로 처치 전, 후 실험군과 대조군 간의 차이를 나타내며, 특정 사건 처치 후 실험군이 다른 조건에 비해 얼마나 더 변화했는지를 통해 처치의 순수한 효과를 추정한다.
-
Yit: i번째 단위에서 t번째 시점의 결과 변수.
-
β0: 상수항.
-
β1: 처치로 인한 효과.
-
Postt: 특정 사건 처치 변수
(처치 후 시점은 1, 개입 전 시점은 0).
-
β2: 실험군과 대조군 간의 기본적인 차이.
-
Treati: 실험군과 대조군 구분변수
(실험군은 1, 대조군은 0).
-
τ: DID 추정치로 처치의 효과.
-
Dit: DID 상호작용 항(처치 후 시점의 실험군은 1, 그 외 0(Postt × Treati).
-
εit: 오차항.
기본 DID 방법을 패널 데이터(panel data)에 적용할 때, 시간과 개체(예: 개인, 기업, 지역 등) 간 존재하는 고유한 특성을 고려하지 않으면, 결과 추정에 편향이 발생할 수 있다. 시간에 따른 고유한 특성은 특정 시기에 모든 개체에 공통적으로 영향을 미치는 요인으로, 어떤 정책의 효과를 평가할 때, 경제 상황에 따라 모든 개체에 영향을 주어 정책 개입의 효과를 구분하기 어렵게 만들 수 있다. 개체의 고유한 특성은 어떤 정책의 효과를 평가할 때, 지역별 단위에서 지리적 특성에 따라 영향을 주어 정책 개입의 효과를 정확히 파악하는데 어려움을 초래할 수 있다. 이러한 시간과 개체 간 존재하는 고유 특성(고정효과)을 통제하기 위해 시간과 개체들의 2요인 고정효과(two-way fixed effects, TWFE)를 활용한다(손호성, 이재훈, 2018; Wooldridge, 2021).
2요인 고정효과를 DID에 구현하기 위해서는 회귀식에 시간과 개체의 고유한 특성을 아래 식(5)와 같이 계수로 표현할 수도 있다. 시간의 변동에 대해 Postt 변수를 사용하여 특정 처치 전후에 관해서만 설명하고 있지만, 시간별 고정효과(λt)의 상수항을 적용하여 모든 단위에 공통으로 적용되는 시간적 특성(예: 경제 성장률 등)을 통제한다. 그러나 이로 인해 기존 Postt항이 시간별 고정효과에 흡수된다. 또한 단위별 변동에 대해 Treati 변수를 사용하여 실험군과 대조군에 관해서만 설명하지만, 단위별 고정효과(αi) 상수항을 적용하여 각 단위의 고유한 특성(예: 지역적 특성, 위치, 환경 등)을 통제하고, 이로 인해 기존 Treati항이 단위별 고정효과에 흡수된다.
-
β0: 상수항.
-
β1: 처치로 인한 효과.
-
Postt: 특정 사건 처치 변수
(처치 후 시점은 1, 개입 전 시점은 0).
-
β2: 실험군과 대조군 간의 기본적인 차이.
-
Treati: 실험군과 대조군 구분변수
(실험군은 1, 대조군은 0).
-
τ: DID 추정치로 처치의 효과.
-
Dit: DID 상호작용 항
(처치 후 시점의 실험군은 1, 그 외 0)
(Postt × Treati)).
-
λt: t번째 시간의 고정효과.
-
αi: i번째 단위의 고정효과.
-
ε: 오차항.
따라서 효과적으로 2요인 고정효과 모형을 DID에 적용하기 위해서 아래 식(6)과 같이 시간(또는 시점)과 단위(개체) 모두에 대해 평균을 미리 차감한 후 분석하는 모형을 사용한다(demeaning 혹은 double demeaning). 이를 통해 개별 단위와 시간에 따른 변화를 동시에 고려하여, 내적 타당성을 높이고 설명 변수가 결과 변수에 미치는 순수한 영향을 추정할 수 있다(De Chaisemartin & D’haultfœuille, 2023; Imai & Kim, 2021).
DID의 모형에 2요인 고정효과(two-way fixed effects)를 위의 식(6)의 방법을 따르면 아래 식(7)과 같이 종속변수를 해당 효과들을 미리 차감한 모형을 활용할 수 있다(Arkhangelsky et al., 2021; Athey & Imbens, 2022), 따라서 식 (7)에서는 각 항 Postt과, Treati이 제거되며, 상수항 β0도 시간별, 단위별 평균이 제거된 상태이기에 더는 포함되지 않는다. 본 연구에서는 식 (7)을 기본모형으로 활용한다.
통제집단합성법(SCM: Synthetic Control Method)은 Abadie and Gardeazabal(2003)의 연구에서 처음 제안된 방법으로, 스페인의 바스크 지방에서 발생한 정치적 갈등이 경제에 미친 영향을 분석하는 데 사용되었다. 이 연구는 바스크 지방과 유사한 경제적·사회적 특성을 가진 가상의 합성 통제 대조군을 생성하여 바스크 지방의 경제적 성과와 비교하는 방식을 활용하였다. 이후 Abadie et al.(2010)의 연구에서는 1988년에 도입된 캘리포니아의 담배 규제 프로그램이 흡연율에 미친 영향을 평가하기 위해 SCM을 적용하였으며, 정책 도입 전 캘리포니아의 흡연율과 동일한 경향을 보일 수 있도록 대조군 지역들을 가중 평균하여 실험군과 대조군의 오차를 최소화하는 합성 대조군을 생성하는 방법을 제시하였다.
SCM을 통해 생성된 합성 대조군은 정책 개입이 없었을 경우 실험군이 보일 것으로 예상되는 반사실적 결과를 추정하는 데 사용된다. SCM 방법은 정책 개입 이전 기간 동안 실험군과 합성 대조군의 결과가 유사하게 나타나도록 설계되기 때문에, DID와 같은 방법에서 적합한 대조군을 찾는 데 발생하는 한계를 극복하는 데 효과적이다. DID와 비교했을 때, SCM은 비교적 적은 대조군을 사용하여 분석이 가능하며, 시간에 따라 변화하는 관찰되지 않은 변수로 인한 누락 변수 편의(omitted variable bias)로 발생하는 내생성 문제도 효과적으로 해결할 수 있다(Ben-Michael et al., 2022; Billmeier & Nannicini, 2013; Doudchenko & Imbens, 2016; Ferman & Pinto, 2021; Gunsilius, 2023).
정책이 개입된 지역과 그 외 정책이 개입되지 않은 지역이 있다고 가정할 때, 지역은 I+1개의 단위로 1번 단위는 정책이 개입된 지역이며, 정책이 개입되지 않은 지역은 I=2,..., I+1까지 잠재적 비교대상집단(donor pool)으로 구성된다. T기간 동안 수집된 데이터에서 T0는 정책이 개입되기 전 기간에 해당되며, 각 지역 단위 i와 기간 t에 대한 결과 값은 Yit로 보았을 때, 는 정책 개입이 없는 지역의 결과 값(합성대조군), 는 정책 개입이 있는 지역의 결과 값으로 정의된다. 합성대조군은 잠재적 비교대상집단의 가중치 평균으로 정의되며, 정책이 개입된 지역(지역 단위 i=1)의 시간 t에 대한 정책 개입 효과는 t〉T0 일 때, 다음과 같다(Abadie, 2021).
지역 단위 I=1은 정책이 개입된 지역으로 는 관찰 가능하지만 은 관찰할 수 없어 이를 추정하기 위해 정책 개입 전, 잠재적 비교 대상 집단의 여러 지역을 결합하여 정책이 개입된 지역과 차이가 최소가 되는 가중치 W=(w2,....,wI+1)를 적용하며, 수식은 다음과 같다(Abadie, 2021).
실험군과 차이가 최소가 되는 합성대조군을 생성하는 적절한 가중치를 적용하는 방법은 연구의 목표와 데이터의 특성에 따라 달라질 수 있으며, 문제에 적합한 변수들을 통하여 적절한 추정방법을 선택하는 것이 중요하다. 기본적으로는 결과변수들의 차이를 이용하여 최소제곱법(ordinary least square)을 활용한 방법이 많이 활용되는데, 이 방법은 가중치 적용은 직관적이고 쉽게 구현할 수 있는 장점이 있으나 과적합(overfitting)의 위험이 있으며, 대조군 간 다중공선성이 높을 경우 불안정한 가중치 추정이 발생할 수 있다. 이에 따라, L2 정규화 기법을 활용한 Ridge 회귀, L1 정규화 기법을 활용한 Lasso 회귀, 두 개의 방법을 포함한 Elastic Net 등이 제안되어, 합성대조군을 생성하는 데 사용되는 가중치를 보다 신뢰성 있게 제공하는 방법으로 유용하게 활용되고 있다. 이러한 기법들은 다중공선성 문제와 과적합 문제를 해결하면서 보다 안정적인 가중치를 추정할 수 있는 장점을 지닌다(Abadie et al., 2010; Billmeier & Nannicini, 2013; Doudchenko & Imbens, 2016; Ferman & Pinto, 2021).
L1 정규화 기법을 활용한 Lasso 회귀의 경우 합성대조군을 생성할 때, 유사도가 낮은 대조군에 대해 가중치를 0으로 만들어 유사도가 낮은 대조군을 배제함으로써, 변수 선택과 축소의 기능을 제공하며, L2 정규화 기법을 활용한 Ridge 회귀의 경우 합성대조군을 생성할 때, 유사도가 낮은 대조군의 가중치를 0과 유사하게 낮은 값으로 적용하여 대조군 간 다중공선성을 줄이고 대조군 수가 적은 경우에 활용하기 적합한 것으로 나타났다(Doudchenko & Imbens, 2016). 본 연구에서는 합성대조군을 생성할 때, Ridge 회귀 방법을 활용하고자 한다. 또한, 합성대조군의 조합할 때 대조군 간의 convex 조합을 만들기 위하여 가중치는 0보다 큰 값으로 설정하고 합이 1이 되게 한다. 하지만, 본 연구에서는 가중치의 합을 1로 제약하지 않고자 하는데, 이는 합성대조군을 생성할 때, 더 유연하고 실험군과의 차이를 세밀하게 조정하여 대조군이 많은 경우에도 적절한 가중치를 부여할 수 있는 장점이 있다(Doudchenko & Imbens, 2016). 실험군과 차이를 최소화하는 합성대조군을 만드는 수식은 다음과 같다.
이러한 최적화 알고리즘(algorithm)을 거쳐서 정책 도입 지역의 정책 도입 이전의 실험군과 유사한 합성대조군이 도출되고 이들을 활용해서 를 계산하여 SCM의 처치 효과의 추정치를 찾게 된다.
통제집단합성-이중차분법(SDID: Synthetic Difference-in-Differences)은 DID의 특정 사건의 개입 전, 후로 실험군과 대조군의 차이를 비교하는 방법과 SCM의 합성대조군을 통한 반사실적인 추정을 통해 특정 사건의 개입 효과를 추정하는 장점을 결합한 방법으로, 두 방법의 한계를 보완하고 더 정확한 추정을 할 수 있는 방법이다(Arkhangelsky et al., 2021). Arkhangelsky et al.(2021)의 연구에서 제안한 SDID 방법은 합성대조군을 생성할 때, SCM에서 제시한 단위별(지역) 가중치에 시간별 가중치를 적용하여 처치 후 시간 경과에 따른 고유특성도 고려하는 방법이다.
단위별 가중치의 경우 SCM과의 차이점은 SDID는 합성대조군과 실험군의 차이를 DID와 같이 모형 내에 포함시켰지만 단위별 가중치에 기본적 평균 차이를 포함시키지 않고, 절편(w0)이 이를 흡수하도록 하였다는 것이다. 즉, 실험군과 합성대조군의 평행추세 가정만 충족하도록 가중치를 추정하는 것이다. 각 단위에 적용되는 가중치가 0보다 크고 그 합이 1이 되는 제약을 가지며, L2정규화를 활용하여 가중치를 추정하였다. 실험군과 합성대조군의 평행추세를 차이를 최소화하는 단위 가중치 수식은 다음과 같다.
시간별 가중치는 찾는 과정은 합성대조군의 처치 후 기간의 평균 결과를 합성대조군의 처치 전 기간 결과로 회귀 분석하는 과정으로 설명할 수 있다. 이를 적용할 경우 처치 전 기간의 데이터를 적절히 반영하여 처치 후 기간의 예상 결과를 더욱 정확하게 추정할 수 있게 하며, 이는 시간에 따른 변동성을 고려하여, 보다 신뢰성 있는 반사실적인 합성대조군을 생성할 수 있게 한다. 시간 가중치를 통해 처치 전 기간의 데이터 중 중요한 시점을 강조하거나 덜 중요한 시점을 낮게 평가할 수 있으며, 이를 통해 데이터의 변동성과 추세를 보다 효과적으로 반영하여 유연성을 갖춘 모형을 구축할 수 있다. 이는 여러기간 동안 일관되지 않은 추세를 보이는 데이터에서도 효과적으로 적용할 수 있으며, 처치 후 기간과 처치 전 기간의 오차를 최소화하는 시간 가중치는 다음과 같다.
SDID 방법을 통해 만들어진 합성대조군은 실험군과 합성대조군의 차이가 최소가 되는 단위별 가중치 wi와 시간별 가중치 λt 적용하며, 실험군와 합성대조군 의 차이를 통해 처치 효과의 추정치를 산출하며, 수식으로 표현하면 다음과 같다.
SDID가 단위별, 시간별 가중치의 적용에 절편을 허용함에 따라 모형이 더 유연하고 정확하게 데이터의 추세를 따를 수 있게 되었으며, 편향을 줄이고 가중치의 균형을 유지하는데 이점이 있다. 이러한 접근법은 실험군과 대조군 데이터의 특성이 완벽하게 일치하지 않는 경우에 유용하며, 다양한 분석 상황에서 더 신뢰할 수 있는 분석을 할 수 있다. 하지만 더 많은 모수를 활용하게 되기에 DID에 비하여 간명하지 않고, 어떤 경우에는 더 안정적이지 못하거나 결과가 뚜렷이 더 좋다고 할 수 없는 상황도 일어날 수 있다. 본 연구에서는 실제 데이터를 기반으로 여러 가지 상황에서 각 분석 방법이 보이는 차이를 확인해보고 각 분석 방법이 장점을 보이는 상황을 찾아보고자 한다.
Ⅲ. 분석 데이터 및 연구설계
본 연구를 위해 새벽배송 서비스가 운영되고 있는 지역에서 추가 새벽배송 사업자가 진입한 경우, 기존 오프라인 점포 매출액의 변화량을 활용하였다. 분석에 활용한 매출액 데이터는 신용카드 패널 데이터를 사용하였으며, 신용카드 패널 데이터는 점포의 단말기를 통해 점포의 정보와 결제한 고객의 이용기록을 결합하여 기간별, 점포 위치별, 업종별, 이용고객 특성별 등 데이터를 수집할 수 있는 장점이 있다. 분석 대상 지역 중 실험군으로 선정한 지역은 1차 새벽배송을 하고 있는 지방광역도시 중 새로운 2차 새벽배송 사업자가 가장 먼저 진입한 대전광역시 서구와 유성구로 하였다. 대조군으로 선정한 지역은 1차 새벽배송을 원래 시작하였으나 새로운 2차 새벽배송 사업자가 진입하지 않은 광주광역시(5개 구: 광산구, 남구, 동구, 북구, 서구), 부산광역시(6개 구: 금정구, 기장군, 동래구, 북구, 연제구, 해운대구)로 하였으며, 오프라인 점포업태 중 새벽배송의 주요 판매 품목과 겹치는 슈퍼마켓의 일별 매출액 데이터를 활용하였다. 신용카드사에서 제공한 슈퍼마켓의 일별 매출액 데이터는 해당 지역 내 슈퍼마켓 업종을 운영하는 사업자에 대한 정보를 추출한 후, 분석에 필요한 기간 내 매출액과 이용 건수 등의 데이터를 추출하였다. 이후, 개인정보 보호법에 따라 특정 점포의 매출액이 식별되지 않도록 지역 내 특정 기간 동안 발생한 슈퍼마켓의 매출액을 합산하여 데이터를 제공받았다. 매출액 데이터는 지역별로 차이가 있으며, 데이터 분포의 정규성을 높이기 위해 자연로그를 취한 값으로 사용하였다. 분석은 각 실험군 지역별로 별도로 진행하며, 대조군은 공통적으로 활용한다. 실험군을 2개로 한 것은 모형결과의 일반화 가능성을 판단하기 위함이다. 분석 기간은 대전광역시 서구와 유성구 내 새로운 추가 새벽배송 사업자가 진입한 시점인 2021년 5월 1일을 기준으로 2년 전부터 진입 후 6개월 후까지의 기간(2019년 5월 2일~2021년 10월 31일)의 일별 데이터를 사용하였다. 분석에 활용한 데이터는 <표 1>과 같다.
<표 2>는 본 연구에서 분석에 사용된 지역 내 오프라인 슈퍼마켓의 일별 매출액에 대한 기초 통계량을 제시하고 있다. 이 표는 실험군(대전광역시 서구, 유성구)과 대조군(광주광역시 5개 구 및 부산광역시 6개 구)에 대해 분석 기간 내 연도별로 나누어 오프라인 슈퍼마켓의 일별 매출액에 대한 평균, 표준편차, 최소값, 최대값, 그리고 일별 평균 거래건수를 나타낸다. 실험군의 매출액은 2019년 평균 544백만 원에서 2021년에는 420백만 원으로 감소하는 추세를 보였다. 반면, 대조군의 매출액은 상대적으로 일정한 수준을 유지하였다. 실험군과 대조군의 표준편차를 비교해보면 실험군의 매출액 변동성이 낮음을 알 수 있다. 또한, 일별 평균 거래건수는 실험군이 2019년 32,805건으로 가장 많았으나, 2021년에는 22,282건으로 감소하였다. 반면, 대조군의 일별 평균 거래건수는 2019년 17,811건, 2021년 16,231건으로 상대적으로 일정한 수준을 유지하였다.
전반적으로 대조군의 오프라인 슈퍼마켓 매출액 변화와 실험군의 연도별 매출액 규모 및 변화 추세가 상이하게 나타났으며, 이는 현실 데이터를 사용하는 데 있어 발생하는 한계점으로 볼 수 있다. 그러나 본 연구에서 사용하는 SCM과 SDID 방법론은 이러한 한계점을 해결하기 위해 도입된 방법론으로, 대조군 중 평행 추세가 유사한 지역과 유사하지 않은 지역을 구분하여 분석에 활용하였다. 이를 통해 SCM과 SDID 방법의 유용성을 확인하고자 한다.
DID 방법은 전통적으로 정책 효과를 평가하는 데 널리 사용되어 온 방법으로, SCM과 SDID는 DID의 한계점을 보완하는 대안적 방법이다. 이들 방법은 최근 연구에서 많이 활용되고 있으며, 본 연구는 이러한 세 가지 방법을 다양한 상황에서 비교하여 각 방법의 적합성을 평가하고, 특정 상황에서 가장 적절한 방법 선택에 대해 논의하고자 한다.
SCM은 실험군과 유사한 대조군을 합성하여 비교하는 방법으로, 단일 실험군이 존재하는 경우 유용하며, 많은 대조군이 필요하지 않다는 점에DID보다 현실적인 연구 방법으로 평가된다. SDID는 SCM과 DID의 장점을 결합한 방법으로, SCM과 마찬가지로 실험군과 유사한 합성대조군을 생성하는 동시에, 단위별 가중치뿐만 아니라 처치 후 시간에 따른 변화를 고려하여 처치 전 시간에 맞춰 가중치를 부여함으로써 분석 결과의 편향을 제거하고 정밀도를 향상시키는 방법이다. 앞서 설명한 세 가지 방법에 따른 처치 효과 추정치를 산출하는 수식을 비교해 보면, 각 공식의 우변에서 오차 제곱합을 최소화함으로써 가장 적합한 모수들을 찾아내는 최적화 과정을 따르며, 특정 방법에서는 가중치가 사전에 설정되어 활용된다. 연구자가 가장 중점을 두는 부분은 처치 효과인τ에 있으며, 본 연구에서 사용된 분석에 사용된 프로그램은 Facure(2022)의 사이트를 참조하였다.
기존 연구에 따르면, SCM과 SDID 방법은 실험군과 대조군이 평행추세 가정을 충족하지 않는 상황에서도 적용 가능하며, 대조군의 수가 비교적 적은 경우에도 유용하다는 점에서 DID 방법에 비해 강점이 있는 것으로 알려져 있다. 특히, 실험군과 유사한 대조군을 선정할 때, 사전 평행 추세보다는 지역적 특성이 유사한 대조군을 선정함으로써 내적 타당성을 높이거나 외생 변수를 통제할 수 있다. 그러나 이러한 경우 실험군과 대조군 간의 차이가 특정 사건의 처리 효과가 아닌 외부 요인에 의해 발생할 가능성이 있으며, 이로 인해 편향된 추정치가 도출되어 실제 효과를 과대 또는 과소 평가할 위험이 있다(Baker et al., 2022; Kahn-Lang & Lang, 2020). 또한, 현실적인 제약으로 인해 실험군과 사전 추세가 유사한 대조군을 선정하는 과정에서 필요한 모든 변수에 대한 데이터 확보와 많은 대조군 수를 확보하는 것이 어렵기 때문에, 평행추세를 충족하지 않는 대조군이나 소규모 대조군을 활용하는 경우, SCM과 SDID 방법이 DID 방법에 비해 더 안정적인 결과를 제공할 수 있다(Arkhangelsky et al., 2021).
각 방법에 대한 비교를 위해 실험군과 합성대조군의 처치 전 기간에 대한 평행추세 유사성을 확인하고자 한다. 처치 전 기간에 실험군과 합성대조군의 유사성과 평행추세가 잘 맞는다면, 사후 기간에 대한 실험군의 처치 효과가 없었을 경우에 만들어낼 반사실적 데이터를 더 잘 구현하여 순수한 처치 효과를 더 추정할 수 있을 것이라고 생각할 수 있다. 실험군과 합성대조군의 유사성 및 평행추세를 확인하기 위해 유클리디안 거리(euclidean distance), 기울기 비교(slope comparison) 방법을 사용하고자 한다.
유클리디안 거리는 두 점 사이의 직선 거리를 측정하는 방법으로, 시계열 데이터에서는 두 시계열 간의 유사성을 측정하기 위해 각 시점에서의 차이를 계산한 후, 그 차이의 제곱을 합산하고 제곱근을 취하는 방식으로 측정한다. 유클리디안 거리는 그 단순성과 효율성 덕분에 많은 시계열 분석에서 기본적인 유사성 측정 도구로 사용되며, 특히 두 시계열 데이터의 기간이 동일할 경우 적합하다(Serra & Arcos, 2014). 본 연구에서는 처치 전 사전 추세 간의 절대적 차이를 측정하여, 실험군과 합성 대조군의 사전 기간 동안 매출액 변동이 어느 정도 유사한지를 평가하고자 하며, 실험군과 합성대조군의 정규화를 진행한 후 이를 측정하였다. 두 시계열 Χ와 Y가 주어졌을 때, 이들의 유클리디안 거리 d(X,Y)는 다음과 같이 계산된다.
<표 3>에서 보이듯이, 지역 내 새벽배송 업체가 추가로 운영되기 전 기간 동안 실험군과 대조군의 유사성을 비교하기 위해, 슈퍼마켓 매출에 영향을 줄 수 있는 지역적 특성인 인구수, 세대수, 1인 가구수, 연령별 인구수, 지역내총생산(GRDP), 1인당 급여 데이터를 사용하였다. K-평균 군집분석(K-means clustering)을 통해 확인한 유사 지역과 오프라인 슈퍼마켓 매출액 추세에 대한 유클리디안 거리를 기반으로 한 유사 지역을 비교하여, 각각의 방법으로 유사도가 높은 두 개의 지역을 확인하였다. 지역적 특성을 고려하여 대조군을 선정하는 경우와 사전 평행추세를 고려하여 대조군을 선정하는 경우 차이가 있으며, 실제 상황에서의 제약과 지역적 특성을 고려하여 대조군을 선정할 때 발생하는 문제로 인해 특정 사건 이전의 평행추세 조건을 만족하는 대조군을 선정하는 데 어려움이 있다. 이러한 이유로 인해 DID 방법보다는 SCM과 SDID 방법의 활용도가 높다.
| 실험군 지역 | 지역적 특성에 따른(K-means) 유사 지역* | Euclidean Distance(E.D.) 기준 유사 지역** | ||
|---|---|---|---|---|
| 첫 번째 유사지역 | 두 번째 유사지역 | 첫 번째 유사지역 | 두 번째 유사지역 | |
| 대전 서구 | 광주 광산구 | 부산 해운대구 | 광주 서구 | 광주 광산구 |
| 대전 유성구 | 광주 광산구 | 부산 해운대구 | 광주 동구 | 부산 기장군 |
유클리디안 거리에 추가적으로 활용하는 기울기 비교는 처치 전 실험군과 합성대조군의 사전 추세의 변화율을 비교하여, 음의 방향인지, 양의 방향인지 구분하며, 평행추세 가정을 어느 정도 충족하는지 확인하고자 한다. 아래 식 (19)를 실험군과 합성대조군에 각각 적용해서 얻은 을 활용하여 식 (20)을 통해 △β1을 계산한다.
이에 따라, 본 연구에서는 세 가지 방법을 비교하기 위해 모형의 결과 값뿐만 아니라 실험군과 대조군의 사전 기간에 대한 유클리디안 거리와 기울기를 비교하고자 한다. 이는 잠재적 결과 체계의 주요 가정인 반사실적 추정을 위해 특정 사건이나 처치가 발생하지 않았을 경우를 가정한 가상의 시나리오를 만들어내는 것이 중요하며, 사전 기간 동안 실험군과 대조군 간의 평행추세가 어느 정도 유사한지를 측정하는 방식으로 진행된다. 즉, 대조군의 수와 기간을 변동시키며 합성대조군을 다르게 구성하고, 세 가지 모형을 적용하여 각 모형의 모수추정치 τ의 값과 통계적 유의성을 확인하는 한편, 합성 대조군과 실험군 간 사전 기간의 평행추세도 점검한다. 실제 데이터를 사용한 연구에서는 모수추정치 τ의 값과 유의도만으로는 진실을 명확히 알기 어려우므로, 이러한 요소만으로 모형을 평가하기에는 한계가 있다. 따라서 평행추세를 확인하는 작업이 필수적이다.
연구 설계는 첫 번째로, 세 가지 방법을 동일한 데이터 세트를 사용하여 전체적으로 비교를 통해 각 방법의 전반적인 성능을 평가한다. 두 번째로, 처치 전 기간이 비교적 유사한 대조군과 유사하지 않은 경우로 구분하여 대조군 수를 순차적으로 늘려가며 각 방법의 성능을 비교한다. 이를 통해 합성대조군을 생성하는 것이 효과가 있는지를 확인하고자 한다. 마지막으로, 사전 처치 기간의 길이를 조정하여 각 방법의 성능을 평가한다. 이는 사전 처치 기간의 길이가 각 방법의 결과에 어떤 영향을 미치는지를 분석하며, SDID에서 제시한 시간 가중치를 준 것이 효과가 있는지를 확인하고자 한다.
Ⅳ. 연구결과
먼저, 서구와 유성구 내 슈퍼마켓의 매출에 대한 새로운 추가 새벽배송 서비스 진입 후 효과 추정치를 살펴보면, <표 4>에서 나타난 바와 같이 DID, SCM, SDID 세 가지 방법 모두 새벽배송 업체의 진입이 슈퍼마켓 매출에 부정적인 영향을 미쳤음을 보여준다. 그러나 각 방법에서 산출된 추정치에는 다소 차이가 있었다. SCM 방법을 적용한 추정치(서구τ=–.091)는 DID의 추정치(서구τ=–.086)보다 더 큰 영향을 보였으며, SDID의 추정치(서구τ=–.083)는 더 작거나 크게 나타나 변동성이 다소 큰 것으로 나타났다.
| 구분 | τ(Standard Error, S.E.) | p-value* | ||||
|---|---|---|---|---|---|---|
| DID | SCM | SDID | DID | SCM | SDID | |
| 서구 |
–0.086 (0.012) |
–0.091 (0.012) |
–0.083 (0.046) |
0.104 | 0.086 | 0.000 |
| 유성구 |
–0.099 (0.013) |
–0.106 (0.013) |
–0.110 (0.051) |
0.066 | 0.049 | 0.000 |
추가로, 새벽배송 서비스 업체의 진입 효과가 실제 효과인지 아니면 우연에 의한 것인지를 검증하고, 모형 간 유효성을 비교하기 위해 위약 시험(placebo test, permutation test)을 진행하였다. 위약 시험은 기존의 DID, SCM, SDID 방법을 사용한 연구에서 대조군 중 한 개 또는 여러 개의 대조군에 임의로 처리 효과를 부여하거나, 처리 시점을 임의로 변경하여 가상의 실험군을 만드는 방식이다. 그런 다음 각 방법을 통해 추정치를 산출하고, 몬테카를로 시뮬레이션이나 부트스트래핑 기법 등을 사용해 100회 이상 반복 측정하여 추정치의 분포를 얻는다. 이를 실제 추정치와 비교하여, 가상의 처리 효과 분포보다 실제 추정치가 더 크거나 작은지에 따라 유효성을 검증한다(Ferman & Pinto, 2019; Krief et al., 2016).
본 연구에서 수행한 위약 시험은 가상의 실험군을 구성하기 위해, 날짜별로 대조군 중 하나를 무작위로 선택하여 슈퍼마켓 매출액 데이터를 추출하는 방식으로 진행되었다. 이후 부트스트래핑 기법을 사용하여 500개의 가상 실험군을 구성하였으며, 각 방법론을 통해 추정치를 도출하였다. 이를 통해 가상 실험군 추정치의 분포와 실제 서구 및 유성구 내 새벽배송 서비스 업체의 진입 효과를 비교한 결과, p-value 값을 산출하였다. 결과는 <표 4>와 같다.
분석 결과에 따르면, 서구의 경우 DID(0.104)는 유의하지 않은 것으로 나타났으며, SCM(0.086)은 신뢰수준 90%에서 유의한 결과를 보였다. SDID (0.000)는 신뢰수준 99%에서 유의한 것으로 나타났다. 유성구의 경우 DID는 신뢰수준 90%에서 유의했고, SCM은 신뢰수준 95%, SDID는 신뢰수준 99%에서 유의한 결과를 보였다. 신뢰수준이 높은(p-value가 작은) 결과일수록 처리 효과가 우연에 의해 발생했을 가능성이 낮으며, 해당 모형이 유효하다는 것을 의미한다.
특히, 추정치의 차이는 사전 기간 동안 실험군과 대조군 간의 평행추세 조건에 따라 영향력이 달라질 수 있음을 시사하며, 이에 대한 평행추세는 <표 5>에서 비교되었다.
| 구분 | Euclidean Distance(E.D.) | Slope Comparison(S.C.)* | ||||
|---|---|---|---|---|---|---|
| DID | SCM | SDID | DID | SCM | SDID | |
| 서구 | 28.00 | 12.63 | 12.31 | –8.66 | –0.58 | –0.58 |
| 유성구 | 26.58 | 17.77 | 16.24 | –8.58 | –0.49 | –0.52 |
<표 5>에서는 실험군과 대조군의 유클리디안 거리 및 기울기 비교 값을 제시하고 있다. DID 방법은 대조군의 평균과 실험군을 비교한 반면, SCM과 SDID 방법은 각 가중치를 통해 생성된 합성대조군과 실험군을 비교하였다. 분석 결과, SCM과 SDID를 통해 추정된 실험군과 합성대조군 간의 유클리디안 거리 값이 DID 방법에 비해 낮은 것으로 나타났다(서구 E.D., DID=28.00, SCM=12.63, SDID=12.31). 또한, 실험군과 대조군 간의 기울기 차이를 살펴보면, SCM과 SDID로 생성된 합성대조군과 실험군 간의 차이가 DID 방법에 비해 적은 것으로 나타났다(서구 S.C., DID= –8.66, SCM=–0.58, SDID=–0.58). 이는 SCM과 SDID 방법이 평행추세 조건을 더 잘 충족시켰음을 의미한다.
<표 6>에서는 세 가지 모형의 적합성과 복잡성을 비교하기 위해 SSE(sum of squared errors) 및 이를 활용한 AIC(akaike information criterion) 값의 비교를 보여주고 있다. AIC는 회귀모형을 평가하는 데 사용되는 지표 중 하나로, 변수 개수, 모형 내 파라미터(parameter)의 개수와 잔차제곱합(sum of squared errors)에 따라 결정되며, 식(21)을 통해 AIC 값을 계산한다.
| 구분 | Sum of Squared Errors(SSE) | Akaike Information Criterion(AIC)* | ||||
|---|---|---|---|---|---|---|
| DID | SCM | SDID | DID | SCM | SDID | |
| 서구 | 6,067.07 | 6,059.44 | 6,059.26 | –521.70 | –507.97 | 221.83 |
| 유성구 | 6,114.68 | 6,114.82 | 6,114.26 | –470.29 | –448.14 | 281.25 |
식 (21)의 AIC 계산 중 k은 모형에서 사용된 파라미터의 수로 DID는 3개(독립변수의 계수 개수(3)), SCM은 14개(독립변수의 계수 개수(3)+대조군별 가중치 적용(11)), SDID는 379개(독립변수의 계수 개수(3)+대조군별 가중치 적용(11)+시간별 가중치 적용에 따른 새벽배송 진입 전 기간(365)).
AIC 값을 비교해보면 서구에서는 DID(AIC: –521.70), SCM(AIC: –507.97), SDID(AIC: 221.83) 순서로 낮았으며, 유성구에서도 비슷한 유형을 보였다. SSE 값을 살펴보면, 서구의 경우 DID: 6,067.07, SCM: 6,059.44, SDID: 6,059.26으로 나타났다. 세 모형의 SSE 값이 유사하며, SCM과 SDID가 DID에 비해 약간 더 나은 성과를 보인다. 유성구에서도 유사한 SSE 값을 보이고 있다. AIC는 모형의 설명력과 복잡성을 고려하며, 낮은값을 가질수록 좋은 모형임을 알려준다. 일반적으로 설명력이 좋은 모형이 많은 모수를 갖게 되는 것을 패널티를 주어서 간명한 모델에 더 좋은 평가를 하게 된다. <표 6>의 결과를 보면, DID 모형이 세 가지 모형 중 가장 적합하고 단순한 모형으로 평가된다. 하지만, SSE값은 세가지 방법 모두 유사하거나 SCM, SDID 방법이 DID 방법보다 낮은 것을 확인할 수 있다. 본 연구와 같은 인과추론연구에서 DID, SCM, SDID 방법과 같은 모형을 비교할 때, AIC가 낮은 것이 좋기는 하지만, 많은 양의 자료가 존재하고, 최종목적이 간명하면서 좋은 모형을 찾는 것이 아닌 모형의 해석 가능성과 처치 효과의 이해를 얻기 위한 것이라면, 연구자가 연구목적에 따라 참고로 활용하면 될 것이다.
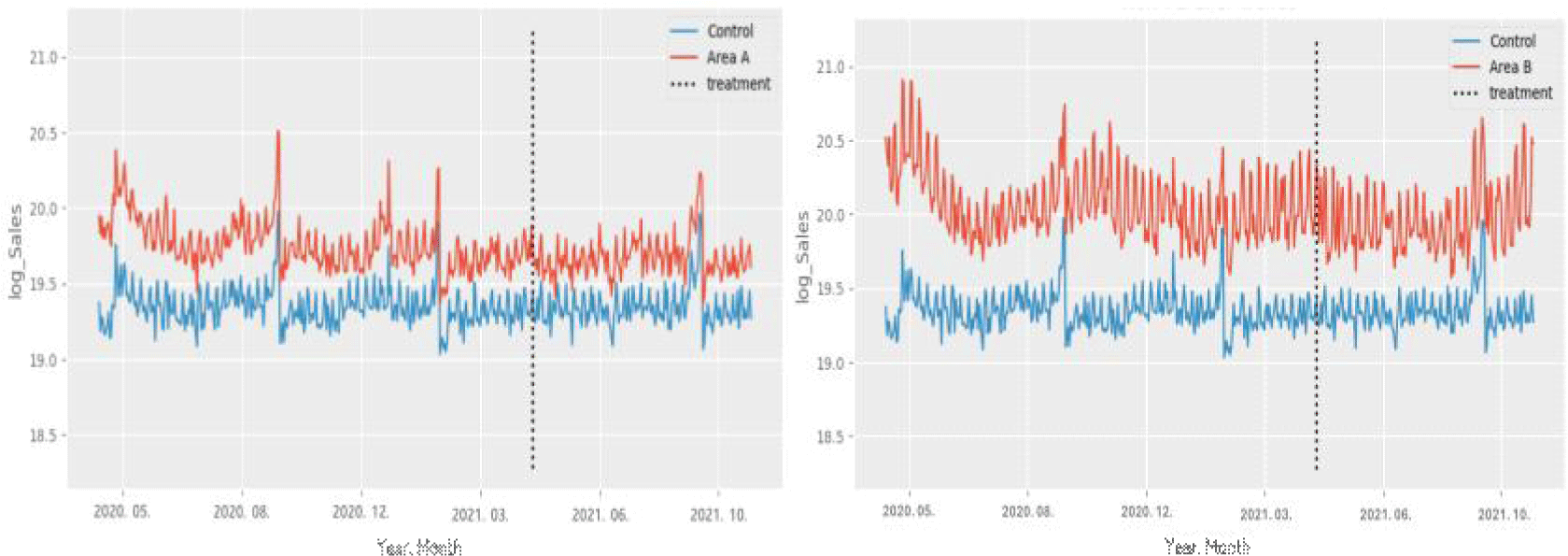
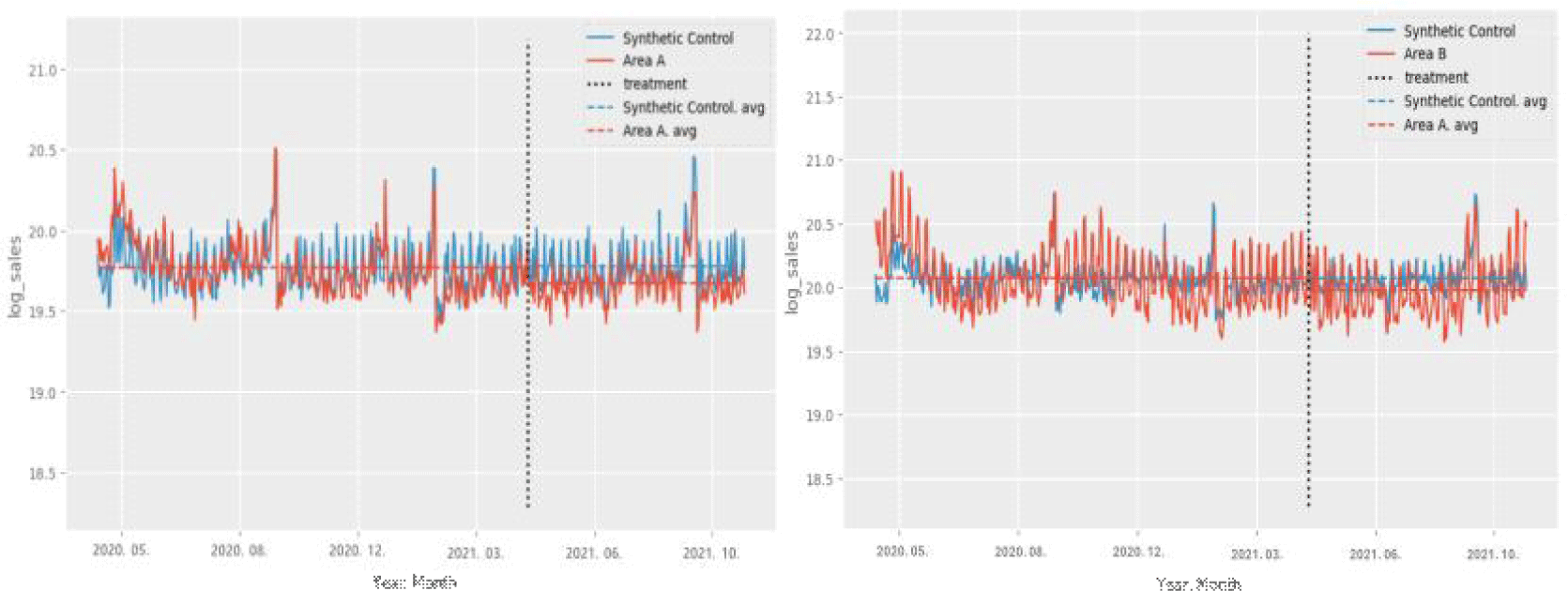
아래의 그림들을 통해 자세히 살펴보면, <그림 1>은 실험군과 대조군의 평균 매출액 변화를 나타내고 있으며, 실험군 지역의 경우 매출액이 전반적으로 감소하는 추세를 보이는 반면, 대조군은 비교적 유지되는 것으로 나타났다. 이러한 실제 데이터를 활용할 경우 편향이 발생할 가능성이 있으며, 사전 기간에 대한 평행추세 조건을 충족하지 못하는 상황이 발생할 수 있다. <그림 2>는 SCM 방법을 통해 생성된 합성대조군과 실험군의 매출액 변화를 보여주며, SCM은 실험군과 거의 유사한 합성대조군을 생성한 것으로 나타났다. 이를 통해 사전 기간에 대해 평행추세 조건을 충족시킴으로써, 새벽배송 업체가 실험군 지역에 진입하지 않았을 경우의 매출액 변화를 예측할 수 있게 되며, 진입 효과를 측정하는 데 있어 시간에 따른 외생변수를 통제하는 데 적합한 방법임을 확인할 수 있다.
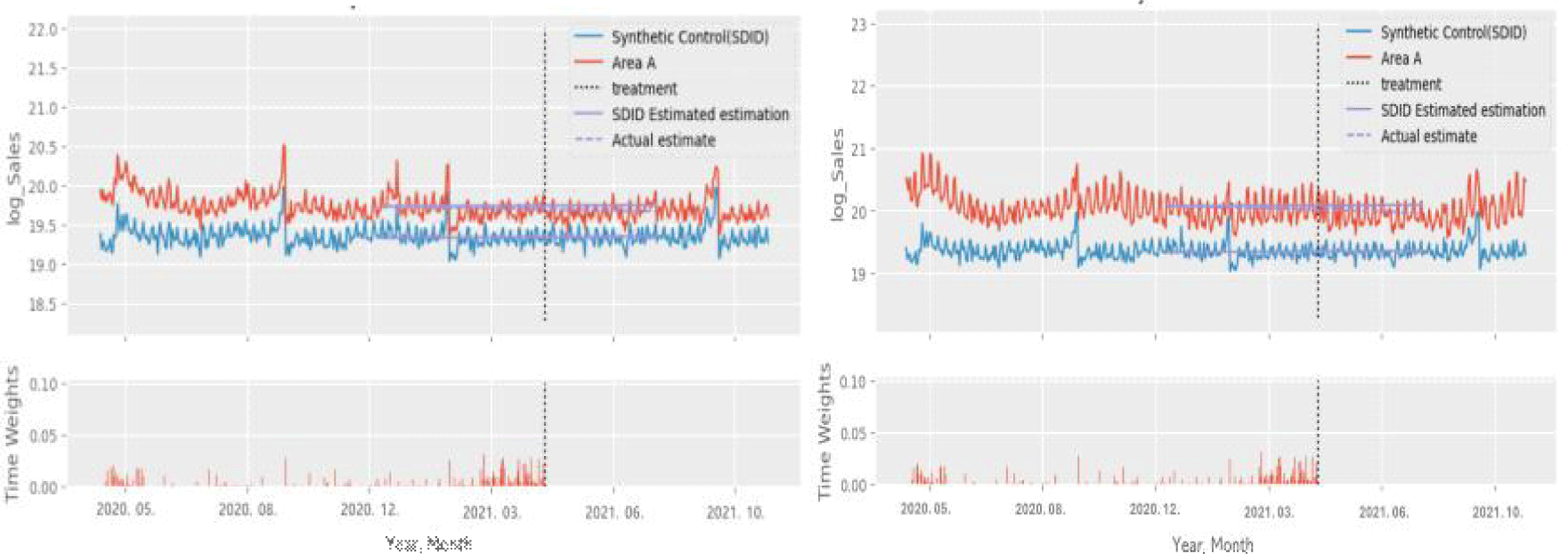
<그림 3>은 SDID 방법으로 생성된 합성대조군과 실험군의 매출액 변화를 나타내고 있으며, SCM과의 차이점은 SDID의 경우 합성대조군이 실험군과 동일한 값을 가지지 않고, 평행추세 조건을 만족시키는 방식으로 단위 가중치가 부여된다는 점이다. 또한, 그래프 아래의 시간 가중치(Time Weights)에서 보이듯이 특정 시점의 가중치를 높게 설정하여 진입 전 특정 시점의 데이터가 진입 후 기간의 결과를 더 잘 예측할 수 있도록 시간 가중치를 부여하였다. 이를 통해 SCM과 마찬가지로 사전 기간에 대해 평행추세를 만족시키면서도, 보다 완화된 결과를 제시하여 특정 시점에서 발생할 수 있는 이상치(outlier)나 변동성을 줄이고, 더 부드러운 추세를 도출할 수 있다.
합성대조군의 장점은 실험군과 유사도가 높은 대조군에 더 높은 가중치를 부여하여, 실험군과 대조군의 평행추세를 바탕으로 개입의 효과를 추정할 수 있다는 점이다. 이는 현실적인 상황에서 평행추세 조건을 충족하지 않는 대조군들에 대해서도 적용 가능하다. 합성대조군을 생성하기 위한 잠재적 대조군 집단의 수가 많을수록, 실험군과 대조군 간의 평행추세를 더 정확하게 형성할 수 있다. 본 연구에서는 대조군을 사전 추세가 높은 대조군과 낮은 대조군으로 구분하여 분석을 진행하였다. 또한, 대조군의 수가 많을수록 적절한 합성대조군을 형성하기가 용이하므로, 대조군의 수를 변화시키며 모형의 성과를 측정하였다. <표 7>에서는 서구와 유성구 지역의 대조군들이 새벽배송 진입 전 매출액 추세와 얼마나 유사한지를 유클리디안 거리로 비교하였으며, 이를 기준으로 사전 추세가 유사한 대조군을 높은 순서로, 유사하지 않은 대조군을 낮은 순서로 분석에 활용하였다.
대조군 수에 따른 분석 결과, <표 8>에 제시된 바와 같이 사전 추세가 유사한 대조군을 사용한 경우, 대조군 수가 증가함에 따라 세 가지 방법에서 추정치 변화의 차이는 크지 않은 것으로 나타났다. 특히, DID 방법을 사용했을 때 표준오차가 가장 낮은 것으로 확인되었다(서구 및 유성구 평균 S.E., DID=0.010, SCM=0.011, SDID=0.047). 반면, 사전 추세가 유사하지 않은 대조군을 사용한 경우, 대조군 수가 증가함에 따라 SCM 방법을 통해 산출된 추정치가 더 낮은 경향을 보였다(서구 및 유성구 사전 추세가 유사하지 않은 대조군 수 3개 평균: DID=–0.101, SCM=–0.101, SDID= –0.088; 7개 평균: DID=–0.095, SCM=–0.092, SDID=–0.100). 특히, SDID 방법의 경우 대조군 수에 따른 추정치의 편차가 크게 나타났다. 전반적으로, 사전 추세가 유사한 대조군을 사용할 경우, 대조군 수와 관계없이 DID 및 SDID 방법의 추정이 안정적인 것으로 확인되었으며, 사전 추세가 유사하지 않은 대조군을 사용할 경우에는 대조군 수가 증가할수록 SCM 방법의 추정이 더 안정적인 것으로 나타났다.
<표 9>에 제시된 바와 같이, 실험군과 대조군을 대상으로 유클리디안 거리와 기울기 비교를 수행한 결과, SCM 및 SDID 방법이 DID 방법에 비해 더 낮은 E.D. 값을 보였다(서구 및 유성구 평균 E.D., DID=26.87, SCM=19.10, SDID=18.94). 또한, 기울기 차이 역시 SCM 및 SDID 방법이 더 작은 것으로 나타났다(서구 및 유성구 평균 S.C., DID=–1.26, SCM=–0.63, SDID=–0.64). 이는 SCM과 SDID 방법을 통해 생성된 합성대조군이 실험군의 반사실적 결과를 더 정확하게 추정할 수 있음을 시사한다.
사전 추세가 유사한 대조군과 유사하지 않은 대조군을 모두 사용한 경우, SCM 및 SDID 방법으로 생성된 합성대조군과 실험군 간의 평행추세는 일반적인 대조군의 평균보다 더 일관성이 높았으며, 실용적인 측면에서도 SCM 및 SDID 방법이 DID 방법에 비해 더 안정적이고 유연한 추정치를 제공하는 것으로 나타났다. 이러한 결과는 정책 평가 및 개입 효과 분석에서 대조군 선정 상황에 따라 적절한 방법을 선택하는 것이 중요함을 보여준다.
세 가지 방법의 이상치 및 변동성에 대한 안정성을 평가하고, 상황에 맞는 적합한 모형을 선택하기 위해 진입 전 기간에 따른 비교를 진행하였다. 진입 전 기간은 2차 새벽배송 업체의 진입 시점을 기준으로 2년 전, 1년 전, 6개월 전, 3개월 전으로 구분하였으며, 이는 사전 진입 기간이 사후 기간보다 긴 경우, 동일한 경우, 짧은 경우에 대한 비교를 위해 설정되었다. 비교에 사용된 대조군 수는 전체 대조군을 활용하였다.
<표 10>의 분석 결과에 따르면, 전반적으로 사전 진입 기간이 긴 2년 전부터 6개월 후까지의 경우, SDID 방법을 통한 추정치(서구 SDIDτ=–0.129, 유성구 SDIDτ=–0.164)가 다른 방법들(서구 DIDτ=–0.159, SCMτ=–0.163, 유성구 DIDτ=–0.188, SCMτ=–0.192)에 비해 낮게 나타났으며, 다른 모형들은 사전 기간이 길어질수록 추정치의 변동 폭이 더 큰 것으로 확인되었다(예: 3개월 전부터 6개월 후까지 서구 DIDτ=–0.022, SCMτ= –0.028, SDIDτ=–0.024로 유사함). 특히, <표 11>에서 나타난 바와 같이, 서구와 유성구 지역 모두에서 SDID는 장기적인 사전 진입 기간 동안 Euclidean Distance와 기울기 비교에서도 일관된 결과를 보였다. 이는 SDID가 사전 진입 기간이 길어질수록 더욱 정확하고 안정적인 추정치를 제공할 수 있음을 시사한다. 반면, 진입 전 기간이 짧은 경우에는 세 가지 모형의 추정치가 유사하게 나타났으나, DID 모형에서는 실험군과 대조군 간의 기울기 비교 값이 크게 나타나, 편향된 결과가 도출될 가능성이 있음을 보여준다.
Ⅴ. 결론
본 연구는 인과추론 연구에서 잠재적 결과 체계 방법으로 사용되는 DID, SCM, SDID 방법의 적용과 각 상황에 따른 적절한 방법 선택에 대해 논의하고자 하였다. 일반적으로 모형 비교를 위해 가상의 데이터를 생성하여 시뮬레이션 연구를 수행하기도 하나, 시뮬레이션 연구는 데이터 생성 과정에서의 가정에 따라 연구 결과가 왜곡될 가능성이 있다. 이에 본 연구는 실제 데이터를 활용하여 시뮬레이션과 유사한 효과를 도출할 수 있는 연구 설계를 채택하였으며, 일부 분석에서는 위약시험을 통해 각 모형의 유효성을 검증하기도 하였다. 연구 대상은 대전시 서구와 유성구 지역에서 2차 새벽배송 업체의 진입이 지역 내 오프라인 슈퍼마켓 매출액에 미친 영향을 분석하였으며, 분석에는 신용카드 패널 데이터를 활용하였다.
분석 결과, SCM과 SDID 방법은 합성대조군을 구성함으로써 실험군과 대조군 간의 유사성을 극대화하여 보다 신뢰할 수 있는 반사실적 가정을 형성하는 것으로 나타났다. 이는 각 대조군에 최적의 가중치를 부여함으로써 실험군의 특성을 잘 반영하는 합성대조군을 생성한 결과이다. 이를 통해 특정 상황에서 SCM과 SDID 방법이 DID 방법보다 더 안정적인 추정치를 제공하는 것을 확인할 수 있었으며, 특히 둘 중 SCM 방법은 대조군의 수가 적은 경우에도 안정적인 결과를 도출하고, 대조군이 개입 전 기간 동안 실험군과 평행추세를 충족하지 않는 경우에도 일관된 결과를 제공하는 것으로 나타났다. SDID 방법은 개입 전 기간이 길어질수록 더 안정적인 반사실적 결과를 도출할 수 있었으며, 이는 다른 방법과 달리 합성대조군을 생성할 때 개입 후 기간에 대한 예측을 개선하기 위해 개입 전 기간 중 중요도가 높은 데이터에 가중치를 부여하는 시간별 가중치가 적용되었기 때문이다. 위약 시험에서도 SDID, SCM, DID 순으로 유의한 결과를 보여주었다.
전반적으로, 개입 전 기간 동안 실험군과 대조군 간의 평행추세가 성립된다고 가정하는 경우, 기본적인 DID 방법을 사용하는 것이 적합한 것으로 나타났다. 이는 SCM과 SDID의 방법은 DID보다 복잡한 계산 과정을 요구하며, 가중치 부여와 같은 추가적인 모형 설정을 포함하기 때문에, 이러한 복잡성은 특정 상황에서 오히려 데이터의 노이즈를 증폭시키거나 모델의 과적합(overfitting)을 유발할 수 있다. 특히, 사전 평행추세가 이미 유사한 경우, 불필요한 가중치 조정으로 인해 모형을 복잡하게 만들어 추정의 정확도가 떨어질 수 있다. 반면, 실제 상황에서 평행추세 가정이 성립되지 않는 경우에는 SCM 및 SDID 방법을 사용하는 것이 보다 적절한 것으로 확인되었다. 특히, 사전 개입 기간이 길수록 SDID 방법을 통해 추정하는 것이 더욱 적합한 방법으로 나타났다.
본 연구는 <표 12>에 제시된 바와 같이, DID, SCM, SDID 방법을 비교 분석함으로써 각 방법의 장단점 및 적합한 적용 상황을 파악할 수 있었다.
특히, 실질적인 환경에서 SCM과 SDID 방법이 DID 방법에 비해 보다 정확한 추정치를 제공할 수 있음을 확인하였다. 이는 SCM과 SDID 방법이 다양한 상황에서 정책 평가 도구로서의 활용 가능성을 높이는 이론적 근거를 제시하며, 개입 전 기간이 길수록 SDID 방법의 성능이 향상됨을 확인함으로써, 장기 데이터를 활용한 분석에서 SDID 방법의 유용성을 강조할 수 있음을 시사한다.
정책 결정자와 데이터 분석가는 본 연구 결과를 바탕으로 더 신뢰성 있는 정책 효과 평가를 수행하는 데 도움을 받을 수 있다. 특히, 대조군의 수가 적고 개입 전 추세가 유사한 경우에는 DID 방법을, 대조군의 수가 많고 개입 전 추세가 유사하지 않은 경우에는 SCM 방법을, 개입 전 기간이 길고 데이터의 변동성이 큰 경우에는 SDID 방법을 사용하는 것이 적절한 것으로 나타났다. 이러한 결과는 실제 환경에서 정책 평가와 같은 특정 사건에 대한 개입 효과를 더 정확하게 추정하고, 이를 바탕으로 의사결정을 내리는 데 기여할 수 있다. 또한, 반사실적 가정을 통해 외생변수를 통제하고 대조군과 실험군 간의 차이를 최소화함으로써 더 신뢰성 있는 결과를 도출할 수 있을 것이다.
본 연구는 기존 연구들의 결과를 바탕으로 실제 데이터를 활용하여 진행되었으나, 실제 데이터가 가지는 한계 역시 존재한다. 본 연구는 특정 지역(서구와 유성구)과 특정 기간에 한정된 데이터를 사용하였기 때문에, 연구 결과를 일반화하는 데에는 한계가 있을 수 있다. 또한, 데이터 수집 과정에서 지역 경제 상황이나 소비자 행동 변화와 같은 외부 요인들을 완벽히 통제하지 못하였으며, 이러한 지역적 특성에 따라 다른 요인을 고려한 추가 연구가 필요하다.
향후 연구에서는 다양한 지역과 기간을 대상으로 데이터를 수집하고 분석함으로써, 본 연구 결과의 일반화를 도출할 필요가 있으며, 다양한 검증을 통해 방법의 안정성을 평가하는 연구가 요구된다. 또한, 지역별 환경에 따른 외부 요인들을 보다 철저히 통제하여 순수한 개입 효과를 더욱 정확히 평가할 수 있는 방법론을 개발하는 것이 중요하다. 이를 통해 인과추론 연구자 및 정책 결정자들에게 더욱 신뢰성 있고 효율적인 방안을 제시할 수 있을 것이다.
본 연구는 새벽배송 서비스의 진입이 오프라인 상권에 미치는 영향을 이해하는 데 중요한 역할을 하였으며, 특히 SCM과 SDID 방법의 실용성과 신뢰성을 입증하는 데 기여하였다. 이러한 결과는 향후 다양한 정책 평가 및 개입 효과 분석에서 SCM 및 SDID 방법의 활용을 더욱 활성화시키는 데 기여할 것으로 기대된다.